Cuando le pedí a ChatGPT su opinión sobre el contenido de este artículo, definió algunas secciones como «intimidantes» y Bard habló de «estadísticas abrumadoras» por lo que se ha realizado un esfuerzo importante por simplificar las explicaciones y hacer accesibles los resultados de todo el análisis. En el prompt final se hace un informe que contiene las conclusiones más relevantes del estudio y que debe ser a lo que prestamos más atención, al menos al principio.
Tabla de contenidos
Introducción
A veces, los alumnos muestran un rendimiento constante, mientras que otros pueden experimentar altibajos en sus calificaciones. Entender estos patrones de rendimiento durante un periodo lectivo puede proporcionar una información importante para diseñar estrategias de enseñanza y aprendizaje más efectivas.
En este artículo, utilizamos dos conceptos estadísticos clave para analizar los patrones de rendimiento temporal de los alumnos: la autocorrelación y la regresión lineal.
Interpretación y significado de la autocorrelación y regresión lineal
En nuestro contexto, la autocorrelación se utiliza para medir si el rendimiento de un alumno en una prueba (examen, ejercicio, trabajo, etc.) está relacionado con su rendimiento en pruebas posteriores a lo largo de un periodo lectivo, es decir, se trata de comprobar la consistencia del rendimiento.
- Rendimiento consistente: Si la autocorrelación es positiva, significa que los alumnos que obtienen buenas notas en una prueba tienden a obtener buenas notas en las pruebas siguientes, y los alumnos que obtienen malas notas en una prueba tienden a obtener malas notas en las pruebas siguientes. En otras palabras, un rendimiento alto se sigue de un rendimiento alto, y un rendimiento bajo se sigue de un rendimiento bajo.
- Rendimiento inverso: Si la autocorrelación es negativa, significa que los alumnos que obtienen buenas notas en una prueba tienden a obtener notas peores en las pruebas siguientes, y los alumnos que obtienen malas notas en una tienden a obtener mejores notas en las siguientes. En otras palabras, un rendimiento alto suele ser seguido de un rendimiento bajo, y un rendimiento bajo suele ser seguido de un rendimiento alto.
- Rendimiento aleatorio: Si la autocorrelación está cercana al cero, esto indica que las notas de una prueba no influyen en las siguientes, siendo los resultados aleatorios entre prueba y prueba.
Importante: ChatGPT realiza un test estadístico para comprobar que el rendimiento no es aleatorio (distinto de 0). Por lo tanto, si no encuentra diferencias significativas, puede clasificar a los alumnos con rendimiento aleatorio, aunque tenga valores positivos o negativos en la autocorrelación.
Por otro lado, la regresión lineal es una técnica que nos permite analizar la relación entre dos variables. En nuestro análisis, utilizamos la regresión lineal para determinar si existe una tendencia en el rendimiento de los alumnos a lo largo del tiempo. La pendiente de la línea de regresión representa esta tendencia:
- Mejorando: Una pendiente positiva indica que las calificaciones de los alumnos están mejorando a lo largo del tiempo,
- Empeorando: Una pendiente negativa indica que las calificaciones están empeorando a lo largo del periodo lectivo.
- Constante: Una pendiente cercana a cero indica que las calificaciones se mantienen relativamente constantes durante todo el periodo lectivo.
Importante: ChatGPT hace un test estadístico para verificar si el rendimiento no es constante (distinto de 0). Por lo tanto, si no encuentra diferencias significativas, puede clasificar a los alumnos con tendencia constante, aunque tenga valores positivos o negativos en la pendiente de la regresión.
Al combinar estos dos enfoques, somos capaces de analizar no solo las tendencias en el rendimiento de los alumnos, sino también la consistencia de estas tendencias. Este análisis nos proporciona una visión más completa de los patrones de rendimiento de los alumnos y puede ayudarnos a identificar estrategias efectivas para apoyar su aprendizaje.
Es importante recalcar que en ningún momento se analiza el rendimiento académico (si las notas son buenas o malas) sino únicamente los patrones temporales del rendimiento, es, pues, un análisis sobre el progreso del alumnado durante un periodo lectivo.
Si estás interesado en el rendimiento académico del alumnado, consulta los artículos: Análisis de los resultados de las calificaciones de múltiples pruebas con ChatGPT-4 y Análisis de los resultados de las calificaciones de una prueba con ChatGPT-4.
Requerimientos
Para realizar este análisis necesitamos:
- ChatGPT-4 con el modo Code Interpreter activado.
- Una serie de notas de los alumnos en una hoja de cálculo, ordenadas cronológicamente, como mínimo se necesitan 3 notas por alumno, pero el análisis mejora con un número mayor.
Estadísticas más relevantes que se llevan a cabo
Si no te interesa la estadística, puedes omitir esta sección y pasar a la siguiente.
- Análisis de series temporales: Corresponde a la autocorrelación y regresión lineal, ya explicados anteriormente. Este análisis permite entender cómo cambian las calificaciones de los alumnos a lo largo del tiempo.
- Para comprobar si las autocorrelaciones son distintas de 0 se usa el test Ljung-Box.
- Para verificar si las pendientes son distintas de 0 se utiliza el test de la t de Student.
- K-means Clustering: Este método de agrupamiento se emplea para dividir a los alumnos en grupos basados en sus patrones de rendimiento a lo largo del tiempo. Los alumnos con patrones similares se agrupan juntos. Esto puede ayudar a identificar grupos de alumnos que podrían beneficiarse de estrategias de enseñanza y aprendizaje similares.
- Análisis de Componentes Principales (PCA): Este es un método de reducción de la dimensionalidad que se usa para visualizar los patrones de rendimiento de los alumnos en un espacio de dos dimensiones. Los alumnos que están más cerca entre sí en este espacio tienen patrones de rendimiento más similares.
- Agrupamiento jerárquico de Ward: Este método de agrupamiento organiza a los alumnos en una jerarquía de grupos basados en sus patrones de rendimiento. Se utilizan las puntuaciones de cada alumno obtenidas en el PCA, se ha hecho así para mantener la coherencia en los resultados. Proporciona una visión detallada de las similitudes y diferencias entre los alumnos.
Preparación de los datos para su análisis
- Los datos deben tenerse en una hoja de cálculo.
- En la primera fila pondremos los títulos de las columnas, estos nombres no deben contener espacios.
- La primera columna estará formada por los nombres de los alumnos sin comas, es preferible que estos nombres sean cortos para mejorar la visualización gráfica. A partir de la segunda columna las notas de los alumnos.
- Estas notas deben estar ordenadas cronológicamente, con las más antiguas en las primeras posiciones.
- Todas las notas deben seguir la misma escala (sobre 10, sobre 100, etc.)
- Si nos falta alguna nota en un alumno, ChatGPT hallará la media de los otros alumnos y se las pondrá a este alumno. Si no deseamos esto podemos eliminar los alumnos a los que les falten notas o completarlas antes de empezar el análisis. No debemos tener nada más en esta hoja de cálculo que los nombres y las notas.
- Descargamos los datos en formato CSV.
- Subimos el archivo CSV en el prompt 1
Prompts
En total son 8 prompts. El análisis es lo suficientemente complejo y extenso como para que ChatGPT no sea capaz de crear un documento de Word con los resultados y conclusiones finales, como hemos hecho en otros análisis. Por lo tanto, si queremos un informe en un documento, habrá que copiar y pegar el texto del informe final en un procesador de textos y los gráficos de alumnos del PCA y dendrograma, copiarlos directamente del historial de la conversación.
Prompt 1
Pedimos a ChatGPT que analice los datos para comprobar si son correctos. Si falta alguna nota en su lugar pondrá la media del resto de alumnos. Si no deseamos hacer esto podemos eliminar al alumno o completar la nota que falta.
En este prompt hay que subir el archivo CSV con los datos ya preparados.
Eres un profesor experto en estadística que me está ayudando con el análisis temporal de los datos de mis alumnos. Por favor, realiza lo siguiente:
1) Carga los datos y realiza un análisis exploratorio inicial para entender la estructura de los datos.
2) Limpia y preprocesa los datos si es necesario, por ejemplo, convirtiendo las calificaciones a formato numérico. Si falta algún valor, calcula la media de la columna.
No calcules estadísticas todavía. Realiza estas tareas y las que te diré más tarde sin interrupciones. Como eres un profesor experto en estadística, si hay que tomar alguna decisión lo harás tú en el momento. Si más adelante escribes alguna tabla, hazlo con formato markdown.
Prompt 2
Cálculo de la consistencia en las notas (autocorrelaciones) y de su tendencia (regresiones) comprobando si siguen un patrón entre una prueba y otra. Donde pone «la misma asignatura» podemos sustituirlo por una explicación más detallada de nuestros datos (por ejemplo: ejercicios de laboratorio de Biología de 1° de ESO).
En este prompt se proporciona una tabla con los patrones de rendimiento de cada alumno, es la tabla más importante del estudio a nivel del alumno.
Estos datos corresponden a notas de la misma asignatura que forman una serie temporal a lo largo de un periodo lectivo, con los datos más antiguos en primera posición.
a) Quiero que realices una autocorrelación con un retraso k=1 para ver la tendencia temporal del rendimiento de cada alumno. Comprueba si las autocorrelaciones son distintas de 0 mediante el test de Ljung-Box.
b) Calcula una regresión lineal para estimar la tendencia en las calificaciones de cada alumno a lo largo del tiempo y comprueba si las pendientes son significativamente distintas de 0.
c) Escribe una tabla Markdown con los siguientes datos:
1) Nombre del alumno
2) Autocorrelación. Etiqueta la columna como: Relación entre una prueba y la posterior (autocorrelación).
3) Una interpretación de una o dos palabras, teniendo en cuenta el resultado del test de Ljung-Box, indicando el significado docente de la autocorrelación:
3.1) Autocorrelación significativamente distinta de 0 y positiva: Rendimiento consistente.
3.2) Autocorrelación significativamente distinta de 0 y negativa: Rendimiento inverso.
3.3) Autocorrelación no significativamente distinta de 0: Rendimiento aleatorio.
4) Pendiente de la regresión lineal. Etiquétala en la columna como: Tendencia del rendimiento (pendiente de la regresión).
5) Una interpretación de una palabra indicando:
5.1) Si la pendiente es significativamente distinta de 0 y positiva: Mejorando
5.2) Si la pendiente es significativamente distinta de 0 y negativa: Empeorando.
5.3) Si la pendiente no es significativamente distinta de 0: Constante.
Prompt 3
Creación de los grupos de patrones de rendimiento según su consistencia y tendencia: Se agrupan los alumnos con patrones de rendimiento similares.
Utiliza el algoritmo de k-means para agrupar a los estudiantes en varios grupos de patrones temporales, utilizando la autocorrelación y las pendientes de la regresión lineal. Ten en cuenta que estas variables tienen unidades diferentes. Utiliza el método Silhouette Score para crear los grupos. Tiene que haber más de 2 grupos. Decide cuántos harás según lo que has obtenido de Silhouette Score y la restricción que te he dado.
Prompt 4
Análisis de los grupos de patrones de rendimiento.
1) En cada uno de los grupos que has creado calcula la autocorrelación de las medias de los alumnos que contiene. Comprueba si las autocorrelaciones son distintas de 0 mediante el test de Ljung-Box
2) En cada uno de los grupos que has creado calcula la regresión lineal de las medias de los alumnos que contiene. Comprueba si las autocorrelaciones son distintas de 0.
Prompt 5
Tabla resumen que permite interpretar los grupos de rendimiento que se han creado.
Analiza los resultados y da un nombre corto con significado educativo a cada grupo, estos nombres cortos no pueden estar repetidos. Revisa los resultados de los alumnos para asignar nombres distintos.
Escribe una tabla Markdown con los siguientes datos:
1) Nombre del grupo.
2) Lista de los alumnos de cada grupo.
3) Autocorrelación. Etiqueta la columna como: Relación entre una prueba y la posterior (autocorrelación).
4) Una interpretación de una o dos palabras, teniendo en cuenta el resultado del test de Ljung-Box, indicando el significado docente de la autocorrelación:
4.1) Autocorrelación significativamente distinta de 0 y positiva: Rendimiento consistente.
4.2) Autocorrelación significativamente distinta de 0 y negativa: Rendimiento inverso.
4.3) Autocorrelación no significativamente distinta de 0: Rendimiento aleatorio.
5) Pendiente de la regresión lineal. Etiquétala en la columna como: Tendencia del rendimiento (pendiente de la regresión).
6) Una interpretación de una palabra indicando:
6.1) Si la pendiente es significativamente distinta de 0 y positiva: Mejorando
6.2) Si la pendiente es significativamente distinta de 0 y negativa: Empeorando.
6.3) Si la pendiente no es significativamente distinta de 0: Constante.
Recuerda: NO puedes repetir los nombres cortos de los grupos
Prompt 6
Gráfico del PCA: Visualización gráfica de los grupos y alumnos según los patrones de rendimiento utilizando ejes de coordenadas.
1) Realiza un análisis de componentes principales de todos los alumnos, usando como datos las autocorrelaciones y las pendientes de las regresiones de cada alumno.
2) Representa gráficamente cada alumno en las dos primeras componentes:
2.1) Utiliza símbolos distintos para cada grupo temporal y escribe los nombres descriptivos que les pusiste en la leyenda del gráfico.
2.2) ETIQUETA cada punto dentro del gráfico con el nombre real del alumno (no uses números) que tienes en los datos originales que subí al principio.
2.3) Identifica los grupos creados con k-means en la gráfica mediante elipses calculadas a partir de las medias y las desviaciones estándar para que cubran el 95% de las observaciones. Antes comprueba si alguna desviación estándar es cero y en ese caso no dibujes elipse para estos alumnos.
3) Dame una interpretación de cada grupo de patrones temporales que me pueda resultar útil como profesor para ayudar a mis alumnos. En cada grupo vuelve a escribir la lista completa de alumnos. Escribe comentarios para los alumnos, especialmente si algún alumno destaca en algún aspecto, positivo o negativo.
Recuerda que en el PCA las etiquetas de los alumnos tienen que ser sus nombres reales, no los identifiques con números.
Prompt 7
Dendrograma: Agrupamiento de los alumnos según la semejanza en sus patrones temporales de rendimiento. El objetivo de este gráfico es el mismo que el anterior, pero usando una visualización diferente y más detallada (aquí no aparecen representados los grupos).
Utiliza el agrupamiento jerárquico aglomerativo con el método de Ward para clasificar a los alumnos utilizando las coordenadas del PCA. Crea un dendrograma con los nombres de los alumnos en el eje VERTICAL para visualizar la agrupación jerárquica de los alumnos.
Prompt 8
Informe final de resultados que deberemos copiar y pegar en un documento de texto, junto con los dos gráficos que se han generado anteriormente.
Vuelve a leer TODA nuestra conversación y escribe un informe final con las conclusiones finales a todo el trabajo que has hecho, centrándote en las pruebas. Estas conclusiones deben servir al profesor para MEJORAR SU PRÁCTICA DOCENTE Y RESOLVER PROBLEMAS. Este informe está dedicado a personas que no saben estadística, por lo tanto, usa un lenguaje sencillo y claro de entender, hazlo en forma de lista. El informe deberá incluir:
1) Una introducción de menos de 110 palabras sobre el propósito de este trabajo (analizar los patrones de rendimiento a lo largo del tiempo) y el significado y repercusiones educativas de las autocorrelaciones (positivas o negativas) y regresiones lineales (mejorar, no cambiar o empeorar) en este contexto.
2) La tabla markdown de todos los alumnos con el nombre del grupo temporal al que pertenecen, las autocorrelaciones, las pendientes de las regresiones, su nivel de significación y las interpretaciones de ambas.
3) La tabla markdown de los grupos de k-mean con la autocorrelación, los alumnos que hay en cada grupo, los coeficientes de la regresión y las interpretaciones de ambos.
4) El gráfico PCA con una breve explicación de cómo se interpreta.
5) El dendrograma con una breve explicación de cómo se interpreta
6) Interpretación de cada grupo de patrones temporales que me pueda resultar útil como profesor para ayudar a mis alumnos. En cada grupo vuelve a escribir la lista completa de alumnos. Escribe comentarios para los alumnos, especialmente si algún alumno destaca en algún aspecto, positivo o negativo. Estos comentarios deben ser útiles, relevantes, profesionales y con ideas concretas para aplicar a las características de cada grupo, si lo necesitas, revisa los datos que tienes sobre cada grupo.
7) Añade cualquier otro aspecto que no he tenido en cuenta en los puntos anteriores y creas que puede ser útil para la mejora de la práctica docente a nivel de profesorado y/o de alumnado y que tenga relación con este trabajo. Han de ser consideraciones concretas basadas en los resultados obtenidos, no escribas recomendaciones generales.
Ejemplo completo
En este ejemplo se han usado nombres ficticios para notas de los deberes de matemáticas de 1º de bachillerato durante todo un año. La conversación mantenida con ChatGPT, excepto gráficos, se puede consultar en este enlace.
Datos utilizados
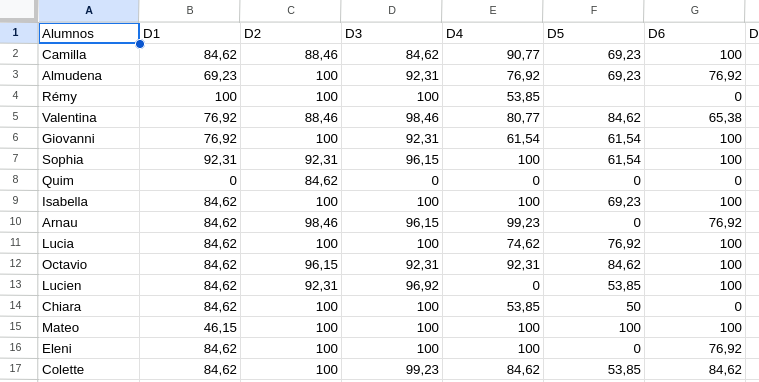
Se exportaron las notas desde Classroom y se eliminaron las columnas de exámenes y otros trabajos que no se querían incluir, se modificó el título de cada columna por otros más sencillos de manejar y por último se cambiaron los nombres por otros y se exportó en formato CSV. El resultado es el siguiente:
Informe final
Este informe se ha obtenido copiando y pegando el resultado del prompt 8, tal como estaba, en un procesador de textos. La imagen del PCA se ha obtenido del prompt 6 y el dendrograma del prompt 7.











Deja una respuesta